lunes, 23 de junio de 2014

DENSIDAD 

En física y química, la densidad (símbolo ρ) es una magnitud escalar referida a la cantidad de masa en un determinado volumen de una sustancia. La densidad media es la razón entre la masa de un cuerpo y el volumen que ocupa.
\rho = \frac{m}{V}\,
Si un cuerpo no tiene una distribución uniforme de la masa en todos sus puntos la densidad alrededor de un punto puede diferir de la densidad media. Si se considera una sucesión pequeños volúmenes decrecientes 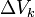\Delta V_k (convergiendo hacia un volumen muy pequeño) y estén centrados alrededor de un punto, siendo \Delta m_k la masa contenida en cada uno de los volúmenes anteriores, la densidad en el punto común a todos esos volúmenes:
\rho(x) = \lim_{k \to \infty} \frac{\Delta m_k}{\Delta V_k} \approx \frac{dm}{dV}
La unidad es kg/m³ en el SI.
Como ejemplo, un objeto de plomo es más denso que otro de corcho, con independencia del tamaño y masa.

Tipos de densidad

Absoluta

La densidad o densidad absoluta es la magnitud que expresa la relación entre la masa y el volumen de una sustancia. Su unidad en el Sistema Internacional es kilogramo por metro cúbico (kg/m³), aunque frecuentemente también es expresada en g/cm³. La densidad es una magnitud intensiva.
\rho = \frac {m}{V}
siendo \rho, la densidad; m, la masa; y V, el volumen de la sustancia.

Relativa

Artículo principal: Densidad relativa
La densidad relativa de una sustancia es la relación existente entre su densidad y la de otra sustancia de referencia; en consecuencia, es una magnitud adimensional (sin unidades)
\rho_r = \frac {\rho}{\rho_0}
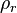donde \rho_r es la densidad relativa, \rho es la densidad de la sustancia, y \rho_0 es la densidad de referencia o absoluta.
Para los líquidos y los sólidos, la densidad de referencia habitual es la del agua líquida a la presión de 1 atm y la temperatura de 4 °C. En esas condiciones, la densidad absoluta del agua destilada es de 1000 kg/m³, es decir, 1 kg/dm³.
Para los gases, la densidad de referencia habitual es la del aire a la presión de 1 atm y la temperatura de 0 °C.

Media y puntual

Para un sistema homogéneo, la expresión masa/volumen puede aplicarse en cualquier región del sistema obteniendo siempre el mismo resultado.
Sin embargo, un sistema heterogéneo no presenta la misma densidad en partes diferentes. En este caso, hay que medir la "densidad media", dividiendo la masa del objeto por su volumen o la "densidad puntual" que será distinta en cada punto, posición o porción "infinitesimal" del sistema, y que vendrá definida por:
\rho = \lim_{V \to 0} \frac {m}{V} = \frac {d m}{d V}
Sin embargo debe tenerse que las hipótesis de la mecánica de medios continuos sólo son válidas hasta escalas de 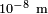\scriptstyle 10^{-8}\ \mathrm{m}, ya que a escalas atómicas la densidad no está bien definida. Por ejemplo el núcleo atómico es cerca de 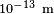\scriptstyle 10^{-13}\ \mathrm{m} superior a la de la materia ordinaria. Es decir, a escala atómica la densidad dista mucho de ser uniforme, ya que los átomos están esencialmente vacíos, con prácticamente toda la masa concentrada en el núcleo atómico.

Aparente y real

La densidad aparente es una magnitud aplicada en materiales porosos como el suelo, los cuales forman cuerpos heterogéneos con intersticios de aire u otra sustancia normalmente más ligera, de forma que la densidad total del cuerpo es menor que la densidad del material poroso si se compactase.
En el caso de un material mezclado con aire se tiene:
\rho_{ap} = \frac {m_{ap}}{V_{ap}} = \frac {m_r + m_{aire}}{V_r + V_{aire}}
La densidad aparente de un material no es una propiedad intrínseca del material y depende de su compactación.
La densidad aparente del suelo (Da) se obtiene secando una muestra de suelo de un volumen conocido a 105 °C hasta peso constante.
Da = {W_{SS}\over V_S}
Donde:
WSS: Peso de suelo secado a 105 °C hasta peso constante.
VS: Volumen original de la muestra de suelo.
Se debe considerar que para muestras de suelo que varíen su volumen al momento del secado, como suelos con alta concentración de arcillas 2:1, se debe expresar el contenido de agua que poseía la muestra al momento de tomar el volumen.

 MEDICION
La densidad puede obtenerse de forma indirecta y de forma directa. Para la obtención indirecta de la densidad, se miden la masa y el volumen por separado y posteriormente se calcula la densidad. La masa se mide habitualmente con una balanza, mientras que el volumen puede medirse determinando la forma del objeto y midiendo las dimensiones apropiadas o mediante el desplazamiento de un líquido, entre otros métodos. Los instrumentos más comunes para medir la densidad son:
  • El densímetro, que permite la medida directa de la densidad de un líquido.
  • El picnómetro, que permite la medida precisa de la densidad de sólidos, líquidos y gases (picnómetro de gas).
  • La balanza hidrostática, que permite calcular densidades de sólidos.
  • La balanza de Mohr (variante de balanza hidrostática), que permite la medida precisa de la densidad de líquidos.
Otra posibilidad para determinar las densidades de líquidos y gases es utilizar un instrumento digital basado en el principio del tubo en U oscilante. Cuyo frecuencia de resonancia está determinada por los materiales contenidos, como la masa del diapasón es determinante para la altura del sonido5



Peso específico


Se le llama peso específico a la relación entre el peso de una sustancia y su volumen.
Su expresión de cálculo es:
\gamma = \frac {P}{V} = \frac {m g}{V}= \rho\ g
siendo,
\gamma\,, el peso específico;
P\,, el peso de la sustancia;
V\,, el volumen de la sustancia;
\rho\,, la densidad de la sustancia;
m\,, la masa de la sustancia;
g\,, la aceleración de la gravedad.

Unidades

  • En el Sistema Internacional de Unidades (SI) se lo expresa en newtons por metro cúbico: N/m3.
  • En el Sistema Técnico se mide en kilogramos–fuerza por metro cúbico: kgf/m3.
  • En el SIMELA se expresa en newtons por metro cúbico: N/m3.
Como el kilogramo–fuerza representa el peso de un kilogramo —en la Tierra—, el valor numérico de esta magnitud, expresada en kgf/m3, es el mismo que el de la densidad, expresada en kg/m3.
Por ende, está íntimamente ligado al concepto de densidad, que es de uso fácil en unidades terrestres, aunque confuso según el SI. Como consecuencia de ello, su uso está muy limitado. Incluso, en Física resulta incorrecto


Publicadas por a la/s

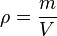
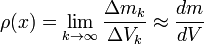
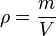
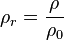
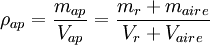
No hay comentarios.:

Publicar un comentario

Suscribirse a: Comentarios de la entrada (Atom)